nanaxprod.blogg.se

If you change the alternate for any situation, you can see the impact on the P-value (the probability of a sample result at least as far away from the null value as that seen in the data, assuming the null hypothesis is true).

The blue arrow shows in which direction the "extreme" values of p̂ will be evidence against the null hypothesis, H 0 in favor of H a. The Normal curve shows the sampling distribution of the sample proportion p̂ when the null hypothesis is true. These concepts easily apply to any other significance test for the center of a distribution. This applet illustrates the P-value for a significance test involving one population proportion, p. Or you can specify the true population proportion and use the NEW SAMPLE button to create a random sample from the population, display the sample count and proportion, and calculate the P-value.Ĭlick the "Quiz Me" button to complete the activity. If you already have a sample, enter the number of "successes" to display the sample proportion on the graph and calculate the P-value. , which will help you assess whether the two sample proportions differ significantly.To set up the test, fill in the boxes: What null hypothesis H 0 about the population proportion p do you want to test? Which alternative (this represents the question) is of interest? How many observations ( n) do you have (30,000 or fewer)? If instead, what you want to do is to compare two sample proportions, you can use this This one proportion z test calculator will allow you to compute the critical values are p-values for this one sample proportion test, that will help you decide whether or not the sample data provides enough evidence to reject the null hypothesis.

The null hypothesis is rejected when the z-statistic lies on the rejection region, which is determined by the significance level (\(\alpha\)) and the type of tail (two-tailed, left-tailed or right-tailed). Null Hypothesis value (): the pre-specified proportion (the value to compare the observed proportion to), expressed as a percentage. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis z(pP) where P is the hypothesized value of population proportion in the null hypothesis, p is the sample proportion, and is the standard deviation of the. In a hypothesis tests there are two types of errors. The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true The sampling distribution used to construct the test statistics is approximately normal

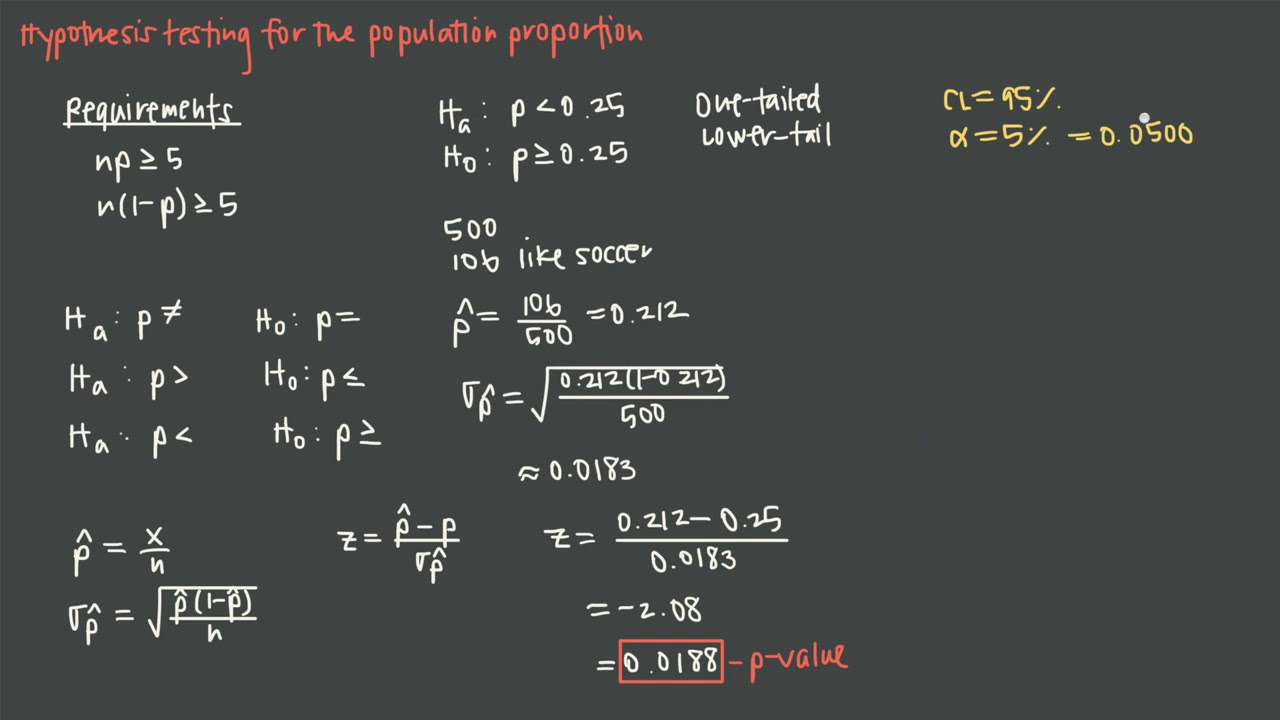
The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true The main properties of a one sample z-test for one population proportion are:ĭepending on our knowledge about the "no effect" situation, the z-test can be two-tailed, left-tailed or right-tailed The null hypothesis is a statement about the population proportion, which corresponds to the assumption of no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis.

The test has two non-overlapping hypotheses, the null and the alternative hypothesis. Please select the null and alternative hypotheses, type the hypothesized. So you can better interpret the results obtained by this solver: A z-test for one proportion is a hypothesis test that attempts to make a claim about the population proportion (p) for a certain population attribute (proportion of males, proportion of people underage). Instructions: This calculator conducts a Z-test for one population proportion (p).